Bạn đang xem bài viết Công thức logarit, tính chất và các dạng toán logarit tại Thcshoanghiep.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Logarit là một trong những chủ đề quan trọng trong toán học, và cũng là một phần đáng chú ý trong giáo dục toán học của học sinh. Với công thức logarit và tính chất của nó, ta có thể dễ dàng giải quyết các bài toán liên quan đến số lớn hay phép tính phức tạp. Hiểu được các dạng toán logarit cơ bản cũng là một điều cần thiết để có thể áp dụng vào thực tiễn khi giải quyết các vấn đề về khoa học kỹ thuật hay tài chính ngân hàng. Trong bài viết này, chúng ta sẽ cùng nhau tìm hiểu về các công thức logarit, tính chất của nó và các dạng toán logarit phổ biến.
Logarit hay Logarithm là chủ đề quan trọng trong chương trình toán học trung học phổ thông. Ghi nhớ logarit giúp giải các bài tập toán một cách chính xác. Bài học dưới đây sẽ cung cấp các thông tin quan trọng về logarit, tính chất, quy tắc và công thức logarit. Hãy cùng theo dõi bài học này giúp ôn tập kiến thức logarit cơ bản và nâng cao trong chương trình toán cấp 3.
Tính chất logarit
Logarit là một hàm logarit học, nó là một trong những phép toán cơ bản trong toán học và được sử dụng rất nhiều trong nhiều lĩnh vực khác nhau, bao gồm toán học, khoa học tự nhiên, khoa học máy tính, và tài chính.
Tính chất của logarit là nó giúp chuyển đổi một tỷ lệ giữa hai số thành một số nguyên. Ví dụ, nếu ta có một số a và một số b, logarit của tỷ lệ a/b sẽ cho ta một số nguyên. Số này có thể được sử dụng để xác định mức độ tăng hoặc giảm của hai số đó so với nhau.
Công thức logarit
Công thức của logarit là:
loga(b) = x
trong đó:
- a là một số dương (base)
- b là một số dương (argument)
- x là một số nguyên (logarithm)
Công thức nói rằng logarit của b theo cơ sở a là x nếu và chỉ nếu a^x = b.
Ví dụ, nếu ta muốn tìm logarit của 100 theo cơ sở 10, ta có thể sử dụng công thức như sau:
10^x = 100 x = 2
Vậy logarit của 100 theo cơ sở 10 là 2.
Các công thức logarit
Có một số công thức quan trọng về logarit, bao gồm:
- Quy tắc cộng: loga(b) + loga(c) = loga(bc)
- Quy tắc nhân: loga(b) + loga(c) = loga(b * c)
- Quy tắc chia: loga(b / c) = loga(b) – loga(c)
- Quy tắc lũy thừa: loga(b^x) = x * loga(b)
- Quy tắc đảo ngược: a^loga(b) = b
- Quy tắc của logarit tự nhiên: log(b) = log(e) * ln(b), trong đó e là số euler.
Chú ý: Trong các công thức trên, a và b là các số dương, x là một số nguyên, và log là logarit tự nhiên.
Công thức đạo hàm logarit
Đạo hàm logarit của một hàm số y = f(x) tại một điểm a là đạo hàm của hàm logarit của f(x) tại điểm a.
Công thức cụ thể của đạo hàm logarithm là:
d/dx (log(f(x))) = f'(x) / f(x)
Trong đó, log là logarithm với gốc mặc định là e, và f'(x) là đạo hàm của hàm số f(x) tại điểm x.
Công thức mũ logarit
Mũ logarithm là một hàm liên quan đến logarithm cơ bản. Nó cung cấp một cách để tính giá trị của một logarithm với gốc bất kỳ.
Công thức chung của mũ logarithm là:
a^b = log_a(b)
Trong đó, a là gốc của logarithm và b là số cần tính logarithm.
Ví dụ, nếu muốn tính logarithm của số 8 với gốc 2, ta có thể sử dụng công thức mũ logarithm như sau:
2^x = 8
Tìm x ta có x = 3. Qua đó, logarithm của 8 với gốc 2 là 3.


Logarit là gì?
Logarit viết tắt là Log là phép toán nghịch đảo của lũy thừa. Logarit một số là số mũ cơ số (giá trị cố định) nâng lên lũy thừa để tạo thành một số khác. Hay hiểu đơn giản hơn thì logarit là một phép nhân được lặp đi lặp lại.
Ai sáng tạo ra thuật toán Logarit? John Napier nhà toán học, vật lý, chiêm tinh học là người phát minh ra logarit.
Tính chất của logarit
Tính chất 1:

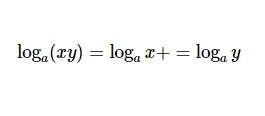
Logarit 2 số x và y nhân với nhau chia thành 2 logarit riêng biệt bằng phép cộng.
Tính chất 2:

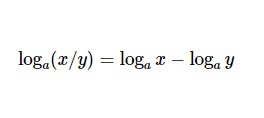
Logarit của 2 số x và y chia cho nhau chia thành 2 logarit bằng phép trừ. Logarit cơ số x sẽ trừ đi logarit cơ số y.
Tính chất 3:

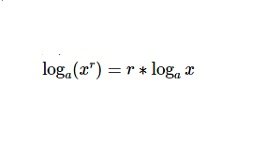
Nếu đối số x của logarit có số mũ r thì số mũ sẽ trở thành số chia cho logarit.
Tính chất 4:

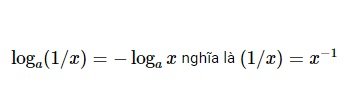
Tính chất 5:

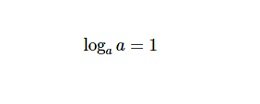
Nếu đối số bằng 1 thì kết quả logarit luôn bằng 0. Tính chất chính xác với bất kỳ số nào có số mũ bằng 0 sẽ bằng 1.
Tính chất 6:

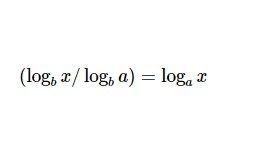
Tính chất còn gọi là biến đổi cơ số. Mỗi logarit chia cho một logarit khác nếu 2 logarit đều có cơ số giống nhau. Lgarit mới sẽ có đối số a của mẫu số biến đổi thành cơ số mới và đối số x tử số trở thành đối số mới.
Công thức logarit
Logarit của một tích
Công thức logarit một tích:

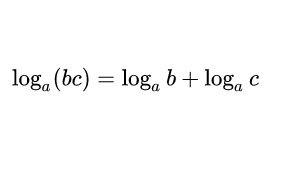
Điều kiện a, b, c đều là số dương và a # 1.
Qy tắc này dùng nhiều bởi các nhà toán học để thực hiện phép nhân hai số thông qua phép cộng logarit, bởi phép cộng dễ tính hơn phép nhân.
Để dùng bảng logarit, người ta đưa về logarit cơ số a = 10, gọi là logarit thập phân, logarit tự nhiên lấy hằng số e (~ 2,718) làm cơ số.
Logarit của lũy thừa

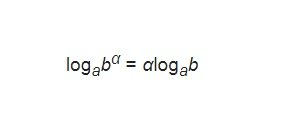
Với điều kiện mọi số α và a, trong đó b là số dương và với a # 1.
Ghi nhớ công thức logarit bằng hình ảnh:


Cách tìm logarit nhanh
Một vài mẹo giúp bạn tìm logarit nhanh và đơn giản đó là:
Chọn bảng đúng: các bảng logarit là logarit cơ số 10 hay logarit thập phân.
Tìm ô đúng: Giá trị ô được xác định ở giao điểm hàng dọc và hàng ngang.
Dễ tìm các số chính xác dựa vào các cột nhỏ bên phải bảng.
Tìm tiền tố trước 1 số thập phân: Bảng logarit giúp chúng ta thấy tiền tố trước một số thập phân.
Tìm phần nguyên. Dễ tìm hơn với logarit cơ số 10. Nếu muốn tìm phần nguyên hãy đếm các chữ số còn lại trong số thập phân và sau đó trừ một chữ số.
Các dạng toán dùng logarit giải
Dạng 1: Dùng định nghĩa và các quy tắc để tính logarit.


Dạng 2: Đưa về cùng cơ số


Dạng 3: Phương pháp đưa về phương trình tích


Cách giải logarit
Dạng 1: Tính giá trị biểu thức, rút gọn biểu thức logarit.
– Bước 1: Biến đổi biểu thức chứa logarit sử dụng tính chất của logarit.
– Bước 2: Tính toán dựa vào thứ tự phép tính.
+ Không có ngoặc: Lũy thừa (căn bậc n) → nhân, chia → cộng, trừ.
+ Nếu có ngoặc: làm trong ngoặc → lũy thừa (căn bậc n ) → nhân, chia → cộng, trừ.
Dạng 2: So sánh các biểu thức chứa logarit.
– Bước 1: Đưa các logarit quay về cùng cơ số.
– Bước 2: Dùng tính chất của logarit để đơn giản hóa biểu thức.
– Bước 3: So sánh biểu thức, vẫn áp dụng tính chất so sánh logarit.
Tính logarit trên máy tính cầm tay
Ngoài cách tính thông thường, chúng ta có thể tính logarit trên máy tính cầm tay. Máy tính CASIO fx570 VN Plus máy tính thế hệ máy mới, thông minh hơn dòng máy tính Casio fx 570ES PLUS giúp giải các bài toán khó.


Ngoài ra còn có máy tính Casio fx570MS còn có thể giải các phương trình bậc 2, bậc 3, đa phương trình cao cấp, đạo hàm, lượng giác,… giải các bài toán logarit cơ bản.
Như vậy chúng tôi vừa gửi đến các bạn học sinh về công thức logarit, tính chất và phương pháp giải các dạng toán logarit thường gặp nhất. Logarit là kiến thức quan trọng trong chương trình toán cấp 3 và xuất hiện nhiều không chỉ trong các bài tập, kiểm tra mà còn trong các kỳ thi quan trọng.
Xem thêm: Các công thức lượng giác
Chúc các bạn học tốt môn Toán!
Trong toán học, công thức logarit là một chủ đề quan trọng và khó khăn đối với nhiều học sinh. Tuy nhiên, với sự hiểu biết về tính chất và các dạng toán logarit, chúng ta có thể áp dụng công thức này nhằm giải quyết nhiều bài toán khó khăn.
Các tính chất logarit thường được đưa ra như tính chất đối xứng, tính chất đồng dạng và tính chất đối số của logarit. Nhờ tính chất này, chúng ta có thể dễ dàng giải các bài toán về phép cộng, phép trừ, phép nhân và phép chia các logarit.
Ngoài ra, các dạng toán logarit phổ biến như tìm số hạng, chứng minh bất đẳng thức đều có thể được giải quyết dựa trên công thức logarit. Điều này cho thấy tính ứng dụng và quan trọng của công thức logarit trong toán học và cuộc sống.
Tóm lại, công thức logarit và các tính chất, dạng toán liên quan đến nó là những kiến thức quan trọng cho môn toán học. Việc nắm vững và áp dụng thành thạo chúng sẽ giúp chúng ta giải quyết nhiều bài toán phức tạp một cách dễ dàng và hiệu quả.
Cảm ơn bạn đã xem bài viết Công thức logarit, tính chất và các dạng toán logarit tại Thcshoanghiep.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Logarit tự nhiên
2. Bất đẳng thức logarit
3. Công thức đổi cơ số logarit
4. Logarit mũ và logarit căn
5. Công thức tổng quát logarit
6. Tính chất của hàm logarit
7. Đồ thị hàm logarit
8. Toán tử đại số với logarit
9. Các bài toán về logarit
10. Ứng dụng của logarit trong thực tiễn.






