Bạn đang xem bài viết Bất đẳng thức Cauchy – Cô-si trong Toán học tại Thcshoanghiep.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Trong toán học, bất đẳng thức Cauchy-Cô-si là một công cụ quan trọng trong việc chứng minh và giải quyết các bài toán liên quan đến tổ hợp và đại số tuyến tính. Bất đẳng thức này không chỉ có ứng dụng rộng trong toán học, mà còn trong nhiều lĩnh vực khác như vật lý, kinh tế, … Trong bài viết này, chúng ta sẽ cùng tìm hiểu các tính chất cơ bản của bất đẳng thức Cauchy-Cô-si và những ứng dụng thực tiễn của nó.
Bất đẳng thức Cauchy hay nhiều người còn gọi là bất đẳng thức Cô-si rất quen thuộc trong Toán học. Trong kiến thức bên dưới chúng tôi sẽ gửi đến các bạn về các nội dung của bất đẳng thức và các các hệ quả, chứng minh minh họa cho bất đẳng thức này. Kiến thức rất cần thiết cho học sinh tham khảo khi bắt đầu bài học hoặc ôn lại kiến thức toán học về bất đẳng thức Cauchy – Cô-si nhanh chóng.

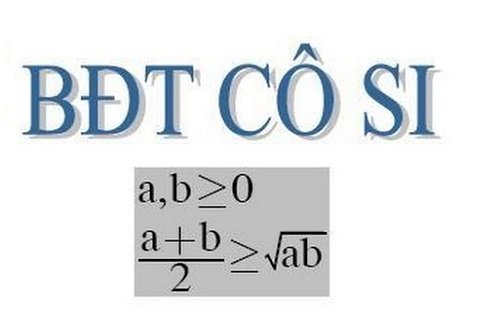
Nội dung bất đẳng thức Cauchy
Bất đẳng thức Cauchy trong toán học là bất đẳng so sánh giữa trung bình cộng và trung bình nhân của n số thực không âm. Nội dung bất đẳng thức chi tiết như sau: Trung bình cộng của n số thực không âm sẽ luôn lớn hơn hoặc bằng trung bình nhân của chúng. Còn trung bình cộng chỉ bằng trung bình nhân khi và chỉ khi n số đó bằng nhau.
Trường hợp 2 số:

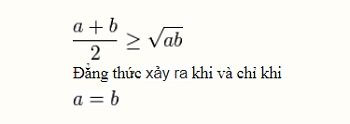
Trường hợp n số:

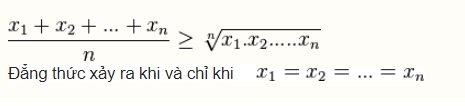
Quy tắc chứng minh bất đẳng thức
Quy tắc song hành: các bất đẳng thức có tính đối xứng, vì vậy chứng minh một cách song hành, tuần tự giúp chứng minh bất đẳng thức.
Quy tắc dấu bằng: dấu bằng = giúp ta kiểm tra tính đúng đắn trong quá trình chứng minh. Dấu bằng giúp định hướng phương pháp giải.
Quy tắc về tính đồng thời của dấu bằng: học sinh khi chứng minh bất đẳng thức thường hay mắc sai lầm. Nguyên tắc áp dụng song hành các bất đẳng thức là điểm rơi phải được đồng thời xảy ra, nghĩa là dấu “ = ” thỏa mãn với cùng điều kiện trong biến.
Quy tắc biên: quy tắc biên thuộc các bài toán quy hoạch tuyến tính, bài toán tối ưu, bài toán cực trị có điều kiện, giá trị lớn nhất nhỏ nhấ.
Quy tắc đối xứng: các bất đẳng thức hay có tính đối xứng, các biến như nhau do đó dấu “ = ” .
Hệ quả bất đẳng thức Cauchy
Hệ quả bất đẳng thức Cauchy được ứng dụng trong việc giúp chúng ta tìm ra các giá trị nhỏ nhất, giá trị lớn nhất của một biểu thức. Hệ quả chia thành 2 như sau:
Hệ quả 1: Nếu tổng hai số dương không đổi thì tích của chúng lớn nhất khi hai số đó bằng nhau.
Hệ quả 2: Nếu tích hai số dương không đổi thì tổng hai số này nhỏ nhất khi hai số đó bằng nhau.
Trung bình có hệ số
Cho n số x1, x2,…, xn ≥ 0 và hệ số α1, α2,…, αn > 0.
Ta đặt:

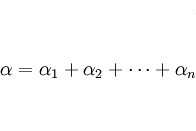
Bất đẳng thức trung bình cộng & trung bình nhân sẽ đúng nếu hai giá trị trung bình có hệ số là như nhau:

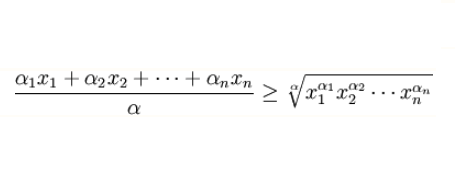
Dấu bằng ” = ” sẽ xảy ra khi và chỉ khi x1=x2=…=xn.
Các loại trung bình khác
Trung bình điều hòa ≤ trung bình nhân ≤ trung bình cộng

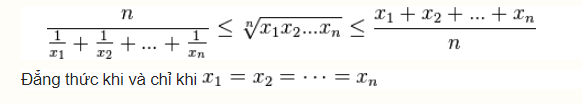
Chứng minh bằng quy nạp
Ta đặt:

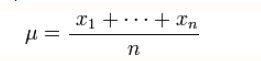
bất đẳng thức tương đương với
x1,…,xn đó là các số thực không âm, ta có:
![]()
![]()
dấu bằng xảy ra và nếu μ = xi với mọi i = 1,…,n.
Chứng minh Cauchy
Khi tất cả giá trị bằng nhau
Nếu tất cả các giá trị bằng nhau: x1=x2=…=xn.
tổng là nx1, giá trị trung bình cộng là x1, tích số dưới căn bậc hai là x1n, iá trị trung bình nhân lúc này là x1. Vế 1 và vế 2 bằng nhau.
Trường hợp giá trị không bằng nhau
Các giá trị bằng nhau không bằng nhau, giá trị trung bình cộng lớn hơn giá trị trung bình nhân. xảy ra khi n> 1.
Với n=2
Nếu n= 2, có 2 giá trị đó là x1 và x2:

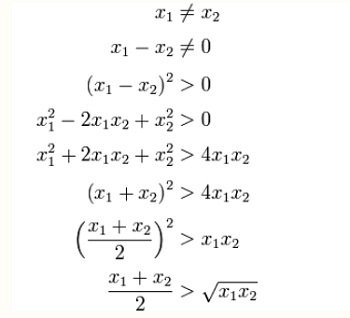
Với n = 2k
Xem n= 2 k, khi k là một số nguyên dương. Tiến hành bằng cách quy nạp toán học.
Trong trường hợp k = 1, tức n = 2, bất đẳng thức được chứng minh.
Khi giá trị k> 1 ất đẳng thức đúng với n = 2k−1, cần chứng minh nó vẫn đúng khi n = 2k.
Với n k
Nếu n không phải hàm mũ tự nhiên cơ số 2, suy ra nó nhỏ hơn một số nào đó theo hàm mũ tự nhiên cơ số 2, vì chuỗi 2, 4, 8,…, 2k,… không bị chặn. Với m giá trị tuân theo hàm mũ tự nhiên cơ số 2 lớn hơn n.
Nếu có n số, biểu diễn giá trị trung bình cộng α và mở rộng:
![]()
![]()
Ta có:


Như vậy:

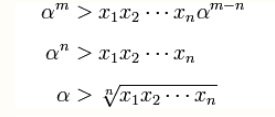
Xem thêm: 7 hằng đẳng thức đáng nhớ
Các bạn vừa theo dõi nội dung về bất đẳng thức Cauchy – Cô-si trong chương trình Toán học trung học. Nắm nội dung và kiến thức về bất đẳng thức sẽ thực hiện tốt các bài tập liên quan và từ đó có điểm cao trong các bài kiểm tra, thi cử. Chúc các bạn học tốt môn toán.
Như vậy, bất đẳng thức Cauchy-Cô-si chính là một trong những bất đẳng thức cơ bản và quan trọng trong toán học. Nó có nhiều ứng dụng trong các lĩnh vực khác nhau như cơ học, điện tử, cơ sở dữ liệu, xác suất thống kê và nhiều lĩnh vực khác. Sự hiểu biết về bất đẳng thức này sẽ giúp cho chúng ta có thể áp dụng hiệu quả vào trong các bài toán thực tế. Bằng cách phân tích và giải thích bất đẳng thức Cauchy-Cô-si, chúng ta có thể thấy rõ sự quan trọng và tầm quan trọng của nó trong toán học.
Cảm ơn bạn đã xem bài viết Bất đẳng thức Cauchy – Cô-si trong Toán học tại Thcshoanghiep.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Bất đẳng thức Cauchy-Schwarz
2. Định lí Cauchy trong đại số tuyến tính
3. Ung thưệ Lagrange
4. Bất đẳng thức Hoelder
5. Bất đẳng thức Minkowski
6. Cô-si trong phân tích hàm
7. Cô-si trong tính toán biến phân
8. Cô-si trong lý thuyết số
9. Cô-si trong phép tính xác suất
10. Công thức đạo hàm của Cauchy-Riemann.






