Bạn đang xem bài viết Cách tính chu vi, diện tích hình thoi tại Thcshoanghiep.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Hình thoi là một trong những hình học cơ bản được sử dụng rộng rãi trong toán học và trong đời sống hàng ngày. Với đặc tính đối xứng và các cạnh bằng nhau, hình thoi được coi là một trong những hình dễ tính toán nhất. Trong bài viết này, chúng ta sẽ tìm hiểu cách tính chu vi và diện tích của hình thoi, thông qua các công thức và ví dụ cụ thể. Hãy cùng tìm hiểu nhé!
Bài học hôm nay chúng tôi xin cung cấp một số kiến thức lý thuyết về cách tính chu vi và diện tích hình thoi. Kiến thức hình học quan trọng dành cho học sinh trung học. Ghi nhớ lý thuyết trong sách giáo khoa và áp dụng vào bài tập trên lớp là cách giúp học sinh có điểm cao trong bài tập cũng như các kì kiểm tra.

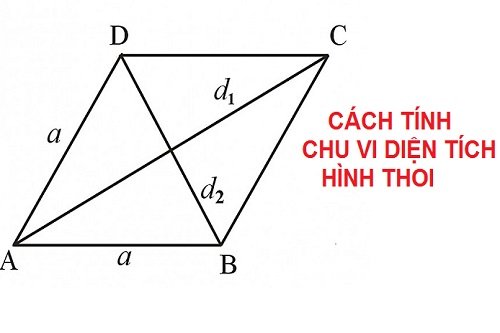
Hình thoi là gì?
Theo khái niệm trên Wikipedia thì hình thoi được định nghĩa là tứ giác có bốn cạnh luôn bằng nhau. Như vậy hình thoi được định nghĩa bằng lý thuyết vô cùng đơn giản và dễ hiểu.
Sau khi hiểu được khái niệm của hình thoi. Chúng ta cùng nhau bắt đầu học thuộc cách tính chu vi diện tích hình thoi trong bài viết bên dưới ngay nhé.
Cách tính chu vi diện tích hình thoi
Tính chu vi hình thoi
Chu vi hình thoi bằng độ dài một cạnh nhân với 4. Số 4 là 4 cạnh hình thoi.
Công thức: P= a x 4
Trong đó:
+ P : Chu vi hình thoi
+ a : cạnh bất kỳ của hình thoi
Ví dụ: Cho hình thoi ABCD có độ dài đường chéo bằng nhau 7cm. Tính xem chu vi của hình thoi là bao nhiêu ?
Có dữ liệu cạnh a = 7cm. Áp dụng công thức P= a X 4 thì ta có chu vi hình thoi đó là: P = a x 4 = 7 x 4 = 28 cm. Suy ra kết quả chu vi hình thoi là 28 cm.
Tính diện tích hình thoi
1. Đo đường chéo
Đo độ dài của các đường chéo trong hình thoi, với đường chéo của hình thoi chính là đường nối của đỉnh đối diện với nhau. Các đường chéo hình thoi vuông góc với nhau tại giao điểm. Xem hình bên dưới để hiểu hơn cách tính đơn giản này nhé.

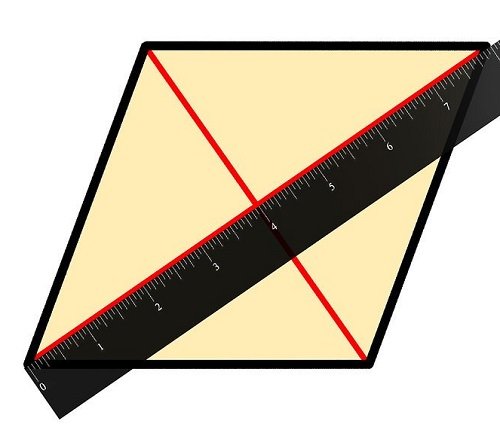
Độ dài mỗi đường chéo là 6 cm và 8 cm kết quả sẽ là 6 x 8 = 48 cm2. Nên nhớ phải chia 2 để có S hình thôi bạn nhé. Từ đó suy ra S hình thoi sẽ là 24 cm2.
2. Tìm độ dài cạnh đáy, chiều cao
Trước tiên nếu tính theo cách này bạn hãy đi tìm độ dài cạnh đáy và chiều cao của hình thoi. Sau đó bạn hãy nhân đáy với chiều cao để có diện tích của hình thoi.

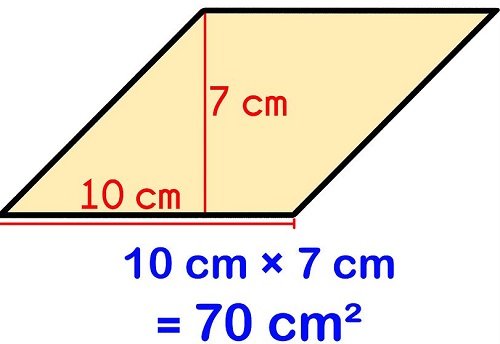
Chẳng hạn hình thoi đáy 6 cm và chiều cao là 8 cm. Khi đã xác định được đáy và chiều cao hình thoi chỉ việc nhân đáy với chiều cao với nhau: 6 cm x 8 cm = 48 cm2. Như vậy kết quả diện tích hình thoi là 70 cm2.
3. Dùng Hệ thức lượng Tam giác
Bình phương độ dài cạnh trong hình thoi. Ví dụ cho hình thoi có các cạnh bằng nhau đó là 2cm, tính ra 2 cm x 2 cm = 4 cm2.
Sau đó hãy nhân giá trị vừa có (4 cm2) với giá trị sin của một trong bốn góc. Ví dụ giá trị 1 góc là 33 độ, nhân sin (33) với 4 cm2 để có giá trị diện tích hình thoi. Thực tế cách làm đó là (2 cm)2 x sin (33) = 4 cm2 x 1 = 4 cm2.
Từ đó suy ra diện tích hình thoi: 4 cm2.
Mô tả giới thiệu chu vi hình thoi
Một hình thoi là một hình bốn cạnh có hai đường chéo bằng nhau và chia hình thành hai tam giác đồng dạng. Để tính chu vi của hình thoi, chúng ta có thể sử dụng công thức: Chu vi = 2 x (đường chéo 1 + đường chéo 2) hoặc Chu vi = 4 x cạnh.
Để mô tả chu vi của hình thoi, chúng ta có thể nói đó là tổng độ dài của các cạnh của hình thoi hoặc là bộ đo đường viền xung quanh của hình thoi. Nếu chúng ta biết độ dài của hai đường chéo của hình thoi, ta có thể tính toán chu vi của hình thoi bằng cách sử dụng công thức trên. Nếu không biết độ dài đường chéo, ta cũng có thể tính chu vi của hình thoi nếu có thông tin về chiều dài của một cạnh.
Chu vi hình thoi có thể được sử dụng trong nhiều lĩnh vực khác nhau như toán học, thiết kế, kiến trúc, v.v. và là một khái niệm cơ bản trong hình học học đường.
Chu vi hình thoi
Để tính chu vi của một hình thoi, chúng ta cần biết độ dài hai đường chéo và chiều dài cạnh của nó (nếu có). Công thức tính chu vi hình thoi như sau:
Chu vi = 2 x (đường chéo 1 + đường chéo 2)
Hoặc
Chu vi = 4 x cạnh
Trong đó, đường chéo 1 và đường chéo 2 là độ dài của hai đường chéo của hình thoi và cạnh là chiều dài của một cạnh của hình thoi.
Ví dụ, nếu đường chéo 1 của hình thoi là 10 cm, đường chéo 2 là 12 cm và không có thông tin về chiều dài cạnh, ta có thể tính chu vi như sau:
Chu vi = 2 x (10 cm + 12 cm) = 44 cm
Nếu chiều dài cạnh của hình thoi là 6 cm, ta có thể tính chu vi như sau:
Chu vi = 4 x 6 cm = 24 cm.
Cách tính chu vi hình thoi
Để tính chu vi của hình thoi, ta cần biết độ dài cạnh của hình thoi hoặc độ dài đường chéo.
Cách 1: Tính chu vi hình thoi bằng cạnh Chu vi hình thoi bằng tổng độ dài của 4 cạnh bằng nhau, vì vậy ta có công thức: Chu vi = 4 x cạnh
Cách 2: Tính chu vi hình thoi bằng đường chéo Chu vi hình thoi bằng tích của đường chéo và hệ số 2 (vì đường chéo là đường chéo của tứ giác, gồm 2 tam giác đều, nên chu vi bằng 2 lần độ dài đường chéo). Ta có công thức: Chu vi = 2 x đường chéo
Ví dụ: Cho hình thoi ABCD có cạnh bằng 5cm và đường chéo bằng 8cm.
- Tính chu vi bằng cạnh: Chu vi = 4 x 5cm = 20cm
- Tính chu vi bằng đường chéo: Chu vi = 2 x 8cm = 16cm.
Công thức tính chu vi hình thoi
Để tính chu vi hình thoi, ta có công thức sau: Chu vi = 2 x đường chéo d
Trong đó, đường chéo d là độ dài của đường chéo của hình thoi.
Nếu hình thoi có độ dài cạnh a, ta cũng có thể sử dụng công thức sau để tính chu vi: Chu vi = 4 x a
Ví dụ: Nếu đường chéo của hình thoi là 8cm, ta có thể tính được chu vi của hình thoi như sau: Chu vi = 2 x đường chéo = 2 x 8 = 16cm.
Tương tự, nếu cạnh của hình thoi có độ dài 6cm, chu vi của hình thoi là: Chu vi = 4 x cạnh = 4 x 6 = 24cm.
Công thức tính chu vi diện tích hình thoi
Công thức tính chu vi hình thoi:
Chu vi (C) = 2 x đường chéo dài (d1 + d2)
Công thức tính diện tích hình thoi:
Diện tích (S) = 1/2 x d1 x d2
Trong đó:
- d1 và d2 là hai đường chéo của hình thoi.
- Các đơn vị đo chiều dài trong công thức có thể được đo bằng đơn vị đo khác nhau, ví dụ như cm, m, mm, inch, feet, v.v. Tuy nhiên, đơn vị đo chiều dài của đường chéo d1 và d2 phải được chọn đồng nhất.
Ví dụ: Cho hình thoi ABCD có đường chéo dài 8 cm và 10 cm. Hãy tính chu vi và diện tích của hình thoi này.
Giải:
- Chu vi hình thoi ABCD = 2 x (8 cm + 10 cm) = 36 cm
- Diện tích hình thoi ABCD = 1/2 x 8 cm x 10 cm = 40 cm2
Cách tính chu vi diện tích hình thoi
Để tính chu vi và diện tích hình thoi, ta có các công thức sau:
- Chu vi hình thoi Chu vi hình thoi bằng tổng độ dài 4 cạnh của hình thoi, nên ta có công thức: Chu vi = 2 x (độ dài cạnh thứ nhất + độ dài cạnh thứ hai)
hoặc
Chu vi = 4 x độ dài 1 cạnh (vì 4 cạnh của hình thoi có độ dài bằng nhau)
- Diện tích hình thoi Diện tích hình thoi bằng tích của hai đường chéo chia cho 2, nên ta có công thức: Diện tích = (độ dài đường chéo thứ nhất x độ dài đường chéo thứ hai) / 2
hoặc
Diện tích = cạnh x cạnh x sin(góc giữa hai đường chéo) (vì góc giữa hai đường chéo bằng 90 độ)
Lưu ý rằng các đại lượng trong các công thức trên phải được đo bằng đơn vị độ dài tương ứng, ví dụ như centimet hoặc mét.
Ví dụ: Giả sử một hình thoi có độ dài hai đường chéo lần lượt là 10cm và 8cm. Ta có thể tính chu vi và diện tích của hình thoi như sau:
- Chu vi = 2 x (cạnh thứ nhất + cạnh thứ hai) = 2 x (10cm + 10cm) = 40cm
- Diện tích = (đường chéo thứ nhất x đường chéo thứ hai) / 2 = (10cm x 8cm) / 2 = 40cm².
Vậy hình thoi này có chu vi là 40cm và diện tích là 40cm².
Chu vi và diện tích hình thoi
Để tính diện tích và chu vi của một hình thoi, ta cần biết chiều dài của hai đường chéo hoặc chiều dài của một đường chéo và một cạnh.
- Diện tích hình thoi:
Công thức tính diện tích hình thoi là: Diện tích = (đường chéo 1 x đường chéo 2) / 2 hoặc Diện tích = cạnh x đường cao
Trong đó, đường chéo 1 và đường chéo 2 là độ dài của hai đường chéo của hình thoi và cạnh là chiều dài của một cạnh của hình thoi. Đường cao của hình thoi là đường thẳng nối hai đỉnh không kề nhau và vuông góc với nhau.
- Chu vi hình thoi:
Công thức tính chu vi hình thoi là: Chu vi = 2 x (đường chéo 1 + đường chéo 2) hoặc Chu vi = 4 x cạnh
Trong đó, đường chéo 1 và đường chéo 2 là độ dài của hai đường chéo của hình thoi và cạnh là chiều dài của một cạnh của hình thoi.
Ví dụ, nếu đường chéo 1 của hình thoi là 10 cm, đường chéo 2 là 12 cm và chiều cao của hình thoi là 8 cm, ta có thể tính diện tích như sau: Diện tích = (10 cm x 12 cm) / 2 = 60 cm² hoặc Diện tích = 8 cm x 12 cm = 96 cm²
Nếu chiều dài cạnh của hình thoi là 6 cm, ta có thể tính chu vi như sau: Chu vi = 4 x 6 cm = 24 cm.
Bài tập hình thoi
Bài 1. Vẽ một tứ giác có độ dài hai đường chéo là: 3,6 cm, 6cm. Hai đường chéo thì vuông góc với nhau. Có thể vẽ được bao nhiêu tứ giác như vậy?
– Tính diện tích mỗi tứ giác.
– Tính diện tích hình vuông với độ dài đường chéo là d.
Giải:
– Vẽ được vô số tứ giác. Ví dụ tứ giác ABCD:
AC = 6cm
BD = 3,6cm
AC ⊥ BD tại H với H là điểm tùy ý thuộc đoạn AC và BD
Diên tích của tứgiác vừa vẽ: SABCD = SABC + SACD =1/2AC.BH + 1/2AC.DH = 1/2AC.(BH +DH) =1/2 AC. BD = 1/2. 6. 3,6 = 10,8 (cm2)
– S.hìnhvuông có độ dài đường chéo là d
Hình vuông có hai đường chéo bằng nhau và vuông góc với nhau, ta suy ra được S = 1/2d.d = 1/2.d2
Bài 3. Hình chữ nhật. Vẽ tứ giác có các đỉnh là trung điểm các cạnh của hình chữ nhật. Giải thích vì sao tứ giác này là hình thoi? So sánh diện tích hình chữ nhật, suy ra cách tính diện tích hình thoi.
Giải:
Cho hình chữ nhật ABCD; M,N,P,Q lần lượt là trung điểm AB,BC, CD, DA.
* Chứng minh MNPQ là hình thoi
Ta có MN = PQ = 1/2BD
NP = MQ = 1/2 AC
Mà AC = BD
⇒ MN = NP = PQ = QM nên tứ giác MNPQ là hìnhthoi (Có 4 cạnh bằng nhau)
* Theo bài 2 (các em tham khảo ở trên), ta có SMNPQ = SABNQ và SMNPQ = SNQDC
Vì vậy SABCD = SABNQ + SNQDC = 2SMNPQ
* Ta có SABCD =2SMNPQ ⇒ SMNPQ = 1/2SABCD = 1/2AB.BC = 1/2NQ.MP
Bài 3. Tính diện tích hình thoi, có cạnh dài 6,2cm và một trong các góc bằng 30o.
Giải:
Giả sử hình thoi ABCD có AB = 6,2cm; A = 30o
Từ B kẻ BH ⊥ AD (H ∈ AD)
Tam giác vuông AHB là một nửa tam giác đều cạnh AB nên:
BH = 1/2 AB = 3,1 (cm)
Suy ra: SABCD = BH.AD = 3,1.6,2 = 19,22 (cm2)
Bài 4. Cho hình thoi ABCD, độ dài AB = 5cm, AI = 3cm (I giao điểm hai đường chéo). Tính điện tích hình thoi.
Giải:
Áp dụng Pi-ta-go vào tam giác vuông IAB, ta có: AB2 = AI2 + IB2
⇒ IB2 = AB2 – AI2 = 25 – 9 = 16
⇒ IB = 4(cm).
AC = 2AI = 2.3 = 6 (cm)
BD = 2IB = 2.4 = 8 (cm)
SABCD = 1/2 AC.BD = 1/2 .6.8 = 24 (cm2)
Bài 5. Hai đường chéo hình thoi có độ dài là 16 cm và 12 cm. Tính diện tích hình thoi và độ dài cạnh hình thoi.
Giải:
– SABCD = 1/2 AC.BD = 1/2 .12.16 = 96 (cm2)
– Trong tam giác vuông OAB, ta có:
AB2 = OA2 + OB2 = AC2 + BD2
= 62 + 82 = 100
AB = 10 (cm)
– Kẻ AH ⊥ CD (H ∈ CD)
Từ đó suy ra: SABCD = AH.CD ⇒ AH = SABCD / CD = 96/10 = 9,6 (cm)
Xem thêm: Cách tính diện tích mét vuông
Rất đơn giản chúng tôi đã hướng dẫn bạn cách tìm chu vi và diện tích hình thoi dễ dàng nhất. Bạn có thể áp dụng cách nào cũng được tùy theo điều kiện thực tế. Ghi nhớ kiến thức trong sách vở và áp dụng vào bài tập sẽ giúp học sinh làm bài tập hiệu quả.
Cảm ơn bạn đã xem bài viết Cách tính chu vi, diện tích hình thoi tại Thcshoanghiep.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Hình thoi
2. Đường chéo hình thoi
3. Công thức tính chu vi hình thoi
4. Công thức tính diện tích hình thoi
5. Đối xứng hình thoi
6. Kích thước cạnh hình thoi
7. Góc nội tiếp hình thoi
8. Góc ngoại tiếp hình thoi
9. Tính chu vi và diện tích hình thoi bằng định lý Pythagoras
10. Tính chu vi và diện tích hình thoi bằng định lý Cosin






