Bạn đang xem bài viết Công thức diện tích toàn phần hình trụ, thể tích, diện tích hình trụ tại Thcshoanghiep.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Hình trụ là một trong những hình học cơ bản được sử dụng trong các bài toán toán học và kỹ thuật. Để hiểu rõ về loại hình học này và tính toán diện tích toàn phần, thể tích và diện tích hình trụ là cần thiết. Việc áp dụng công thức chính xác sẽ giúp chúng ta giải quyết những bài toán liên quan đến hình trụ một cách nhanh chóng và chính xác. Bài viết dưới đây sẽ trình bày cách tính toán diện tích toàn phần, thể tích và diện tích hình trụ để giúp bạn có thể áp dụng nhanh chóng vào thực tế.
Trong SGK các bài tập về hình trụ rất phổ biến. Nhiều giáo viên đưa ra các bài tập liên quan đến hình trụ, để giải các bài tập tốt các em cần nắm kiến thức cơ bản về thể tích hình trụ, diện tích toàn phần hình trụ…Hãy xem các công thức bên dưới để nắm vững hơn kiến thức trước khi thực hiện các dạng bài tập nhé.

Khái niệm hình trụ
Khái niệm cơ bản: Hình trụ là hình giới bạn bởi mặt trụ, với hai đường tròn có đường kính luôn bằng nhau.
Ví dụ: Hình chữ nhật ABCD, với CD là cạnh cố định.
Đường AB là trục.
CD là đường sinh.
Độ dài AB = CD = h (tương ứng với chiều cao hình trụ).
Hình tròn có tâm A. Bán kính r = AD.
Hình tròn có tâm B. Bán kính r = BC. Hai hình tròn tâm A và tâm B là đáy hình trụ này.
Hình trụ tròn xoay:
Hình trụ tròn xoay được tạo thành khi chúng ta quay hình chữ nhật ABCD xung quanh đường thẳng có chứa một cạnh. Ví dụ như cạnh AB thì đường gấp khúc ABCD tạo thành một hình, hình đó chúng ta gọi là hình trụ tròn xoay.
Công thức tính thể tích hình trụ, diện tích hình trụ
Công thức tính diện tích, diện tích toàn phần hình trụ
Diện tích hình trụ: toàn bộ không gian chiếm giữ bằng cách tính tổng diện tích xung quanh và diện tích hai đáy. Diện tích toàn phần hình trụ: diện tích mặt xung quanh hình trụ, không gồm diện tích hai đáy.
– Công Thức Tính Diện Tích Xung Quanh Của Hình Trụ:
S (xung quanh) = 2 x π x r x h
Trong đó với:
r: bán kính hình trụ
h: chiều cao nối từ đáy tới đỉnh hình trụ
Công Thức Tính Diện Tích Toàn Phần Hình Trụ
S (toàn phần) = 2 x π x r2 + 2 x π x r x h = 2 π x r x (r + h)
Trong đó với:
r: bán kính hình trụ
2 x π x r x h : diện tích xung quanh của hình trụ
2 x π x r2: diện tích hai đáy
Bài tập ví dụ:
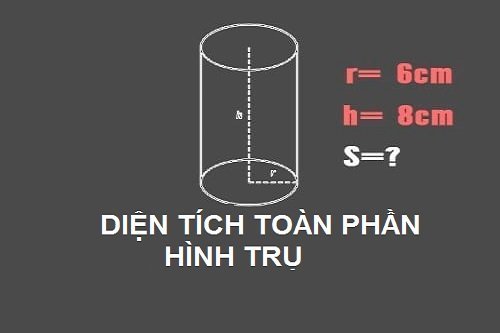
Cho một hình trụ bán kính đường tròn đáy 6 cm , chiều cao nối từ đáy tới đỉnh hình trụ dày là 8 cm. Tính xem thử diện tích xung quanh và diện tích toàn phần hình trụ là bao nhiêu ?
Cần xác định trước tiên đó là bán đường tròn đáy r = 6 cm, chiều cao hình trụ h = 8 cm . Áp dụng công thức tính S xung quanh hình trụ và S toàn thần hình trụ:
– S xung quanh của hình trụ = 2 x π x r x h = 2 x π x 6 x 8 = ~ 301 cm2
– S toàn phần của hình trụ = 2 Π x R x (R + H) = 2 X π x 6 x (6 + 8) = ~ 527 cm2.
Công thức tính thể tích hình trụ
Khái niệm: Thể tích hình trụ là lượng không gian chiếm giữ một hình trụ. Thể tích hình trụ dùng đơn vị đo là lập phương của khoảng cách (mũ 3 khoảng cách).
Tính thể tích hình trụ đơn giản khi sử dụng công thức sau:
V = hπr
Trong đó với:
h là chiều cao
r là bán kính
Bài tập
Cùng giải một số bài tập liên quan đến bài học ngày hôm nay. Chúng tôi còn có một số lời giải cho các dạng bài tập này. Mời các em theo dõi.
Bài 1: Lọ thủy tinh hình trụ chiều cao 15 cm, bán kính phía dưới đáy 5cm. Tìm thể tích lọ thủy tinh.
Thể tích lọ thủy tinh tính bằng công thức sau: V = π r2h = 3.14 x 52 x 15 = 1 177.5 (cm3)
Bài 2: Hình trụ đường kính mặt đáy đó là 12 cm, chiều cao sẽ gấp 3 lần bán kính. Tìm thể tích hình trụ đó.
Bán kính đây: r = d/2 = 12/ 2 = 6 (cm)
Chiều cao hình trụ: h = 3r = 3 x 6 = 18 (cm)
Thể tích hình trụ: V = π r2h = 3.14 x 62 x 18 = 2034.72 (cm2)
Bài 3: Hãy tìm thể tích hình trụ khi biết chu vi đáy bằng 25 dm và chiều cao hình trụ này là 6 dm.
Bán kính hình trụ: r = C/ 2π = 25 / (2 x3.14) ≈ 4 (dm)
Thể tích hình trụ: V = π r2h = 3.14 x 42 x 6 = 301.44 (dm3)
Bài 4: Hình chữ nhật ABCD có AB = 10 cm, BC = 15 cm. Quay hình chữ nhật quanh cạnh BC. Tìm thể tích hình trụ.
Thể tích hình trụ: V = π r2h = 3.14 x 102 x 15 = 4712.39 (cm3)
Bài 5: Cho hình chữ nhật ABCD với chiều dài AB và chiều rộng BC 16 cm. Chiều dài gấp ba lần chiều rộng. Xoay hình chữ nhật quanh cạnh AB. Hãy tìm thể tích hình trụ.h.
Chiều dài hình chữ nhật AB = 16 / (3+1) x 3 =12 (cm)
Chiều rộng hình chữ nhật BC = 16 – 12 = 4 (cm)
Hình trụ có r = 4 cm và h = 12 cm
Thể tích hình trụ: V = π r2h = 3.14 x 42 x 12 = 602.88 (cm3)
Thể tích lọ thủy tinh: V = π r2h = 3.14 x 52 x 15 = 1 177.5 (cm3)
Xem thêm: Công thức về mũ – logarit
Vừa rồi là công thức tính diện tích toàn phần hình trụ, diện tích xung quanh hình trụ và công thức tính thể tích hình trụ vô cùng đơn giản và dễ hiểu đúng không nào các bạn? Chỉ với việc nắm vững các công thức tính căn bản trên đây sẽ giúp làm được các bài tập bên trong SGK và các bài tập nâng cao hiệu quả nhất.
Chúc các bạn học tốt môn Toán.
Tổng kết lại, công thức diện tích toàn phần và thể tích của hình trụ là rất quan trọng trong việc tính toán và ứng dụng trong thực tế. Diện tích toàn phần của hình trụ bao gồm hình tròn đáy và mặt bên, còn thể tích hình trụ là tổng thể tích của hình tròn đáy và mặt trụ. Việc áp dụng công thức đúng cách và hiểu rõ các tính chất của hình trụ sẽ giúp chúng ta giải quyết các bài toán liên quan đến hình trụ một cách nhanh chóng và chính xác. Công thức này còn được áp dụng rất nhiều trong các ngành kỹ thuật như xây dựng, cơ khí, địa chất và trong lĩnh vực giảng dạy. Vì vậy, học sinh và sinh viên nên nghiên cứu và áp dụng công thức này một cách hiệu quả trong học tập và trong thực tiễn để đạt được kết quả tốt nhất và phát triển năng lực của mình.
Cảm ơn bạn đã xem bài viết Công thức diện tích toàn phần hình trụ, thể tích, diện tích hình trụ tại Thcshoanghiep.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Hình trụ
2. Công thức diện tích toàn phần hình trụ
3. Công thức thể tích hình trụ
4. Diện tích xung quanh hình trụ
5. Đường tròn đáy hình trụ
6. Chiều cao hình trụ
7. Bán kính hình trụ
8. Diện tích cơ bản hình trụ
9. Thuật ngữ hình học: hình trụ
10. Hình trụ trong không gian 3 chiều






