Bạn đang xem bài viết Bảng công thức đạo hàm nguyên hàm đầy đủ chi tiết tại Thcshoanghiep.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Bảng công thức đạo hàm nguyên hàm là một công cụ hữu ích cho những người học toán, đặc biệt là trong lĩnh vực tích phân. Bảng này bao gồm tất cả các công thức cần thiết để tính toán đạo hàm và nguyên hàm của các hàm số phổ biến nhất. Trong bài viết này, chúng ta sẽ cùng tìm hiểu về bảng công thức đạo hàm nguyên hàm và các bước cơ bản để sử dụng nó hiệu quả.
Đạo hàm nguyên hàm là kiến thức toán học quan trọng xuất hiện trong chương trình trung học phổ thông. Đây là các kiến thức quan trọng mà học sinh phải nắm vững nhằm giải toán chính xác, hiệu quả. Cùng ôn tập kiến thức qua bảng công thức đạo hàm nguyên hàm đầy đủ chi tiết mà chúng tôi đề cập bên dưới. Chắc chắn sẽ hữu ích và cần thiết cho các bạn học sinh.


Đạo hàm là gì?
Trong toán học, đạo hàm của hàm số là mô tả sự biến thiên của hàm số tại một điểm cụ thể nào đó. Đạo hàm là một khái niệm cơ bản trong chương trình toán học giải tích.
Nguyên hàm là gì?
Trong giải tích thì nguyên hàm hàm số thực cho trước f là một hàm F có đạo hàm bằng f, vậy F′ = f. Quá trình chúng ta đi tìm nguyên hàm gọi là tích phân bất định. Xác định biểu thức cho nguyên hàm khó hơn so với việc tìm đạo hàm.
Bảng công thức đạo hàm cơ bản
Học sinh cần ghi nhớ bảng công thức đạo hàm cơ bản áp dụng cho các bài toán cơ bản.


Hai hàm phân thức hữu tỉ có đạo hàm:

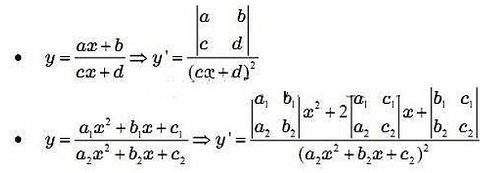


Quy tắc đạo hàm của hàm số hợp: Nếu y = y(u(x)) thì y'(x) = y'(u) . u'(x).
Đạo hàm của hàm số sơ cấp


Bảng đạo hàm cấp cao:

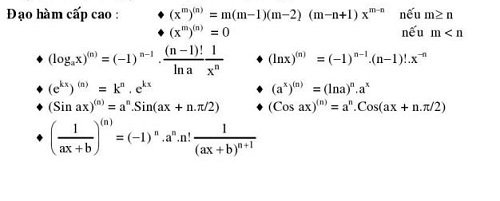
Bảng công thức nguyên hàm
Tính chất của nguyên hàm:

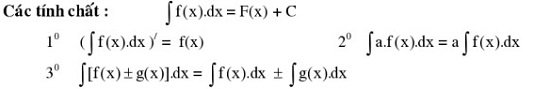
Bảng nguyên hàm cơ bản

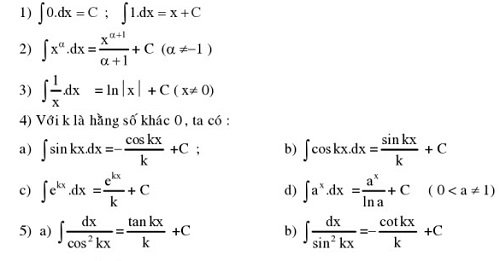
Bảng nguyên hàm mở rộng

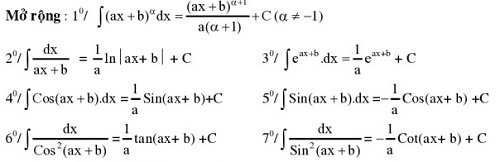
Phương pháp đổi biến số:

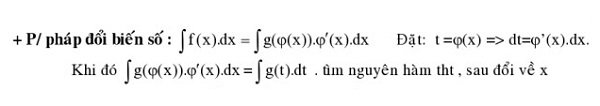
Phương pháp tích phân từng phần:

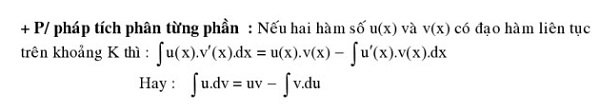
Mẹo ghi nhớ đạo hàm
Đạo hàm với các công thức thường gây khó khăn cho học sinh, vì vậy bài thơ bên dưới sẽ giúp các bạn ghi nhớ tốt hơn phần đạo hàm.










Bài thơ được sáng tạo nhằm giúp các em học sinh ghi nhớ tốt bảng đạo hàm, từ đó giải toán hiệu quả và chính xác.
Các dạng toán nguyên hàm
Bài toán 1: Phương pháp đổi biến số dạng 1 tìm nguyên hàm I = ∫f(x)dx
* Phương pháp:
– Bước 1: Chọn x = φ(t), φ(t) là hàm số chúng ta chọn.
– Bước 2: Lấy vi phân 2 vế, dx = φ'(t)dt.
– Bước 3: Biểu thị f(x)dx theo t và dt: f(x)dx = f[φ(t)].φ'(t)dt = g(t)dt.
– Bước 4: I = ∫g(t)dt = G(t) + C
Bài toán 2: Phương pháp đổi biến số dạng 2 tìm nguyên hàm I = ∫f(x)dx
* Phương pháp:
– Bước 1: Chọn t = ψ(x), với ψ(x) là hàm số phù hợp.
– Bước 2: Vi phân 2 vế: dt = ψ'(x)dx.
– Bước 3: Biểu thị f(x)dx theo t và dt: f(x)dx = f[φ(t)].φ'(t)dt = g(t)dt.
– Bước 4: I = ∫g(t)dt = G(t) + C
Các bạn vừa theo dõi bảng công thức đạo hàm nguyên hàm đầy đủ và phương pháp ghi nhớ đạo hàm qua bài thơ. Các dạng toán nguyên hàm và phương pháp giải hiệu quả. Các kiến thức này rất quan trọng với học sinh 12, hãy nắm vững kiến thức và ôn tập để giải các bài toán một cách hiệu quả và điểm số cao trong kiểm tra.
Xem thêm: Các công thức lượng giác
Chúc các bạn học tốt môn Toán!
Như vậy, thông qua bài viết về bảng công thức đạo hàm nguyên hàm, chúng ta đã được định nghĩa về đạo hàm và nguyên hàm, cũng như các công thức đạo hàm cơ bản và đầy đủ chi tiết. Bảng công thức này là một công cụ quan trọng để giải các bài toán trong lĩnh vực tính toán và khoa học tự nhiên nói chung. Việc thuộc lòng các công thức trong bảng này giúp các bạn dễ dàng áp dụng để giải quyết các bài toán sử dụng đạo hàm nguyên hàm một cách nhanh chóng và chính xác. Việc hiểu rõ và học tập các công thức trong bảng này sẽ giúp cho các bạn thành công trong việc học và nghiên cứu các lĩnh vực khoa học tự nhiên liên quan đến đạo hàm và nguyên hàm.
Cảm ơn bạn đã xem bài viết Bảng công thức đạo hàm nguyên hàm đầy đủ chi tiết tại Thcshoanghiep.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Đạo hàm nguyên hàm
2. Bảng công thức đạo hàm
3. Bảng công thức tích phân định nghĩa
4. Chi tiết công thức lượng giác
5. Các phương pháp tính đạo hàm
6. Định nghĩa nguyên hàm và đạo hàm
7. Tính tích phân bằng phương pháp tích phân không xác định
8. Tính diện tích dưới đồ thị hàm số
9. Các công thức đạo hàm của các hàm cơ bản
10. Ứng dụng của đạo hàm và nguyên hàm trong toán học và các ngành khoa học khác






