Bạn đang xem bài viết Công thức & diện tích toàn phần hình nón tại Thcshoanghiep.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Hình nón là một trong những hình học cơ bản mà chúng ta đã học từ nhỏ. Đây là một hình dạng cực kỳ phổ biến trong khoa học và toán học, và cũng được ứng dụng trong những lĩnh vực khác nhau của cuộc sống hàng ngày. Trong bài viết này, chúng ta sẽ tìm hiểu về công thức và diện tích toàn phần của hình nón. Điều này không chỉ giúp chúng ta cải thiện kiến thức toán học, mà còn giúp cho việc tính toán và ứng dụng trong cuộc sống trở nên dễ dàng hơn. Hãy cùng tìm hiểu nhé!
Các bạn muốn ôn lại kiến thức về hình nón, công thức và cách tính diện tích toàn phần của hình nón để áp dụng trong học tập, trong công việc hay trong cuộc sống. Vậy mời các bạn cùng tham khảo bài viết dưới đây để biết công thức & cách tính diện tích toàn phần hình nón.

Dưới đây Thcshoanghiep.edu.vn.vn chia sẻ đến các bạn khái niệm hình nón, công thức và cách tính diện tích toàn phần hình nón, mời các bạn cùng theo dõi.
Hình nón là gì?
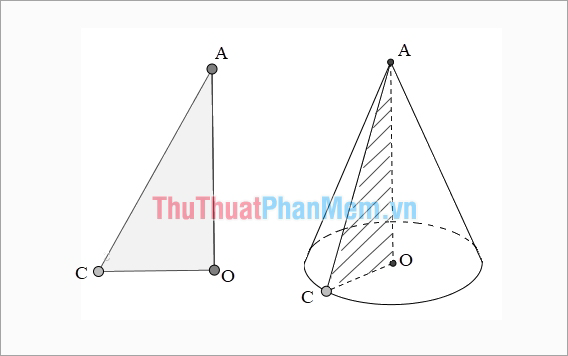
Khi ta quay tam giác vuông OAC một vòng quanh cạnh góc vuông OA cố định thì ta được hình nón. Như vậy hình nón được tạo bởi:
- Cạnh OC tạo nên đáy hình nón là một đường tròn tâm O.
- Cạnh AC quét lên mặt xung quanh của hình nón, mỗi vị trí của nó được gọi là một đường sinh.
- A là đỉnh của hình nón và AO là đường cao của hình nón.
Công thức tính diện tích toàn phần hình nón
Giả sử các bạn có hình nón như sau:
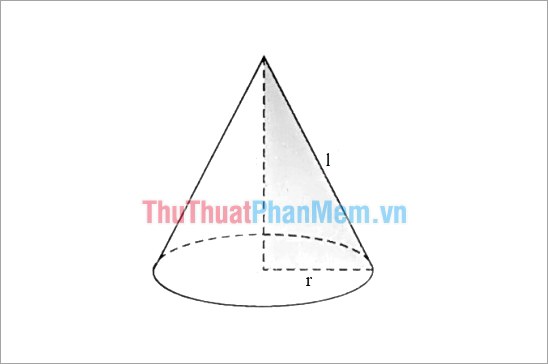
Diện tích toàn phần của hình nón bằng diện tích xung quanh của hình nón cộng với diện tích đáy. Công thức tính diện tích toàn phần:
({S_{tp}} = {S_{xq}} + {S_đ} = pi rl + pi {r^2})
Trong đó:
- ({S_{tp}}) là diện tích toàn phần của hình nón.
- ({S_{xq}}) là diện tích xung quanh của hình nón.
- ({S_{đ}}) là diện tích đáy của hình nón.
- π là hằng số (=3.14159265359)
- r là bán kính mặt đáy của hình nón.
- l là độ dài đường sinh của hình nón.
Cách tính diện tích toàn phần hình nón
Để tính diện tích toàn phần của hình nón các bạn cần biết diện tích xung quanh và diện tích đáy của hình nón, hoặc nếu chưa biết thì các bạn cần biết bán kính r và độ dài đường sinh l.
- Nếu biết diện tích xung quanh và diện tích đáy hình nón hay nếu đã biết bán kính r và độ dài đường sinh l thì các bạn chỉ cần áp dụng công thức ({S_{tp}} = {S_{xq}} + {S_đ} = pi rl + pi {r^2})
- Nếu chưa biết bán kính r và đường sinh l của hình nón thì các bạn cần tính r và l dựa vào những gì đề bài cho.
- Sau khi đã tính bán kính r và đường sinh l thì các bạn sử dụng công thức tính diện tích toàn phần hình nón ở trên để tính.
Ví dụ: Cho hình nón có độ dài đường sinh là 10 cm, độ dài đường cao là 6 cm. Tính diện tích toàn phần của hình nón.
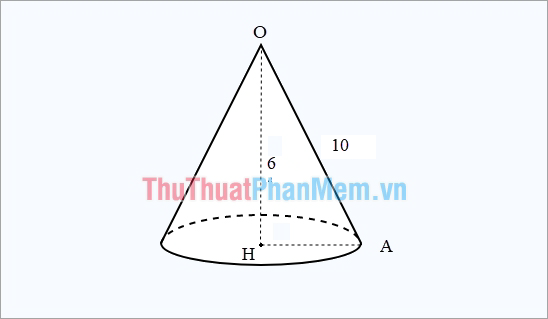
Giả sử hình nón có đỉnh là O, tâm đáy là H, A là một điểm thuộc đường tròn đáy. Như vậy ta sẽ có: OA = 10 cm, OH = 6 cm.
Trong tam giác vuông OHA, (r = HA = sqrt {O{A^2} – O{H^2}} = sqrt {{{10}^2} – {6^2}} = 8cm)
Áp dụng công thức tính diện tích toàn phần hình nón ta có:
({S_{tp}} = pi rl + pi {r^2} = pi .8.10 + pi {.8^2} = 80pi + 64pi = 144pi )
Như vậy diện tích toàn phần hình nón là (144pi c{m^2}).
Như vậy trên đây bài viết đã chia sẻ đến các bạn công thức và cách tính diện tích toàn phần của hình nón, hi vọng các bạn sẽ ghi nhớ công thức và áp dụng cách tính diện tích toàn phần hình nón để áp dụng vào các bài tập hay trong cuộc sống.
Trong kết luận, ta có thể rút ra những điểm chính sau đây:
– Công thức và diện tích toàn phần của hình nón là những khái niệm quan trọng trong toán học và hình học, được sử dụng rộng rãi trong các bài toán và ứng dụng thực tế.
– Công thức tính diện tích toàn phần của hình nón rất đơn giản, chỉ cần nhân bán kính đáy với chu vi đáy và cộng với diện tích xung quanh, đây cũng là một cách để vận dụng kiến thức đơn giản về toán học vào thực tế.
– Để sử dụng được công thức tính diện tích toàn phần của hình nón, ta cần phải biết rõ các thông số về bán kính đáy, chiều cao và chu vi đáy của hình nón đó. Do đó, việc tính toán được diện tích toàn phần có thể giúp chúng ta rút ra những kết luận quan trọng về hình dạng của hình nón đó.
– Tuy nhiên, cần lưu ý rằng công thức và diện tích toàn phần chỉ áp dụng cho hình nón có đáy là hình tròn, nếu đáy của hình nón không phải là hình tròn thì cần có các công thức tính toán khác phù hợp.
– Trong nghiên cứu toán học và hình học, công thức và diện tích toàn phần của hình nón còn có các ứng dụng quan trọng trong việc tính toán thể tích của các hình học phức tạp hơn nữa, đặc biệt là trong công nghệ xây dựng, kiến trúc và khoa học vật liệu.
Cảm ơn bạn đã xem bài viết Công thức & diện tích toàn phần hình nón tại Thcshoanghiep.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Nguồn Bài Viết: http://thuthuatphanmem.vn/cong-thuc-dien-tich-toan-phan-hinh-non/






