Bạn đang xem bài viết Công thức tính thể tích hình trụ, cách tính thể tích hình trụ chính nhanh và chính xác tại Thcshoanghiep.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Hình trụ là một trong những hình học cơ bản mà chúng ta thường gặp trong cuộc sống và trong lĩnh vực toán học. Việc tính toán thể tích hình trụ là một công việc quan trọng trong nhiều lĩnh vực như xây dựng, địa chất, khoa học vật liệu và cách tính thể tích hình trụ chính xác và nhanh chóng là điều không thể thiếu. Trong bài viết này, chúng ta sẽ cùng tìm hiểu về công thức tính thể tích hình trụ và những cách tính đơn giản và chính xác nhất để giải quyết vấn đề này.
Hình trụ là hình mà ai cũng có thể thấy trong cuộc sống, nhưng để tính thể tích hình trụ thì không phải ai cũng biết công thức tính thể tích hình trụ. Nếu các bạn muốn biết công thức tính thể tích hình trụ hay cách tính thể tích hình trụ nhanh và chính xác nhất thì các bạn hãy cùng tham khảo bài viết dưới đây.

Dưới đây thuthuatphanmem.vn chia sẻ đến các bạn công thức tính thể tích hình trụ và ví dụ cụ thể cách tính thể tích hình trụ nhanh và chính xác nhất, mời các bạn cùng theo dõi.
Mục Lục Bài Viết
Khái niệm hình trụ
Hình trụ là hình có hai đáy là hai đường tròn song song và bằng nhau.
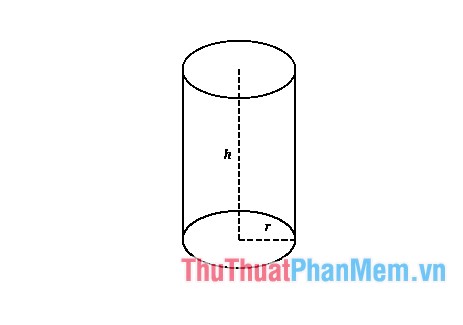
Công thức tính thể tích hình trụ
Thể tích hình trụ được tính bằng diện tích đáy nhân với chiều cao.
[V = {S_{đáy}} cdot h = pi {r^2}h]
Đơn vị đo thể tích chuẩn là mét khối (({m^3})).
Trong đó:
- V là thể tích hình trụ.
- ({S_{đáy}}) là diện tích đáy của hình trụ
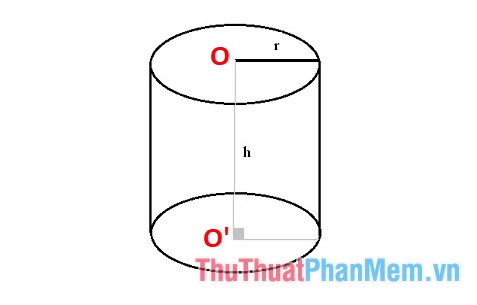
- r là bán kính hình tròn đáy.
- h là chiều cao hình trụ (khoảng cách giữa hai đáy O và O’).
- (pi ) là hằng số toán học (( sim 3,14)).
Ví dụ cách tính thể tích hình trụ
Ví dụ 1: Tính thể tích hình trụ biết bán kính mặt đáy r = 6 cm; chiều cao hình trụ h = 8 cm.
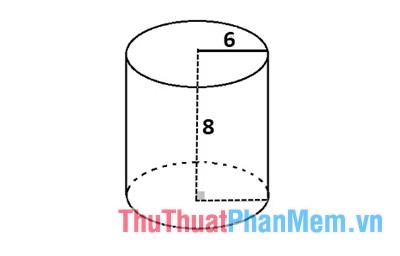
Giải:
Các bạn chỉ cần áp dụng công thức tính thể tích:
[V = pi {r^2}h]
Ta có:
[V = pi {6^2}8 = 288pi ]
Vậy thể tích hình trụ là (288pi left( {c{m^3}} right))
Ví dụ 2: Tính thể tích hình trụ biết đường kính đáy bằng độ cao của hình trụ d = h = 8 cm.
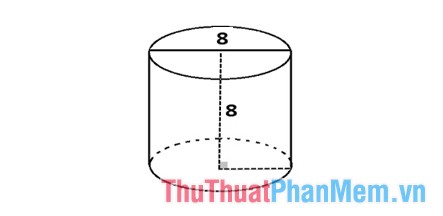
Vì đề bài cho đường kính (ký hiệu là d) của mặt đáy nên các bạn chỉ cần chia giá trị này cho 2 để được bán kính r vì d = 2r.
➩ r = 8 : 2 = 4 cm.
Áp dụng công thức tính thể tích ta có:
[V = pi {r^2}8 = pi {4^2}8 = 128pi ]
Vậy thể tích hình trụ là (128pi left( {c{m^3}} right)) hay ({ sim 402c{m^3}})
Trên đây thuthuatphanmem.vn đã chia sẻ đến các bạn công thức tính thể tích hình trụ và ví dụ cụ thể giúp các bạn hiểu rõ hơn cách tính thể tích hình trụ. Hi vọng qua bài viết này các bạn có thể nhớ công thức và biết cách tính thể tích hình trụ để áp dụng trong học tập cũng như trong công việc, cuộc sống hàng ngày. Chúc các bạn thành công!
Như vậy, thông qua bài viết trên, chúng ta đã nắm được công thức tính thể tích hình trụ và cách tính thể tích hình trụ chính nhanh và chính xác. Tính thể tích hình trụ là một kỹ năng toán học cơ bản đối với học sinh phổ thông, nhưng lại vô cùng quan trọng và ứng dụng rộng rãi trong cuộc sống hàng ngày, đặc biệt trong ngành kỹ thuật, xây dựng và vật lý. Vì vậy, việc nắm vững cách tính thể tích hình trụ là điều không thể thiếu đối với những ai muốn phát triển sự nghiệp của mình trong các lĩnh vực này.
Cảm ơn bạn đã xem bài viết Công thức tính thể tích hình trụ, cách tính thể tích hình trụ chính nhanh và chính xác tại Thcshoanghiep.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Nguồn Bài Viết: http://thuthuatphanmem.vn/cong-thuc-tinh-the-tich-hinh-tru-cach-tinh-the-tich-hinh-tru-chinh-nhanh-va-chinh-xac/






