Bạn đang xem bài viết Các công thức lượng giác đầy đủ, dễ nhớ nhất tại Thcshoanghiep.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Trong toán học, lượng giác là một chủ đề quan trọng về hình học và các ứng dụng thực tế trong cuộc sống. Các công thức lượng giác đầy đủ và dễ nhớ sẽ giúp cho các bạn có thể tính toán các giá trị lượng giác một cách dễ dàng và chính xác. Trong bài viết này, chúng tôi sẽ giới thiệu đến các bạn một số công thức lượng giác cơ bản và quan trọng nhất. Hãy cùng đọc và học hỏi nhé!
Các công thức lượng giác nằm trong chương trình toán học, rất cần thiết khi học sinh giải toán. Công thức lượng giác bao gồm các công thức cơ bản và các công thức biến đổi nâng cao. Để giúp học sinh ghi nhớ hoặc ôn tập lại kiến thức toán học chúng tôi xin giới thiệu bảng công thức lượng giác đầy đủ, chi tiết và dễ nhớ nhất dành cho học sinh.


Trong bất cứ bài thi phương trình lượng giác sẽ xuất hiện. So với các câu hỏi khác phương trình lượng giác câu hỏi dễ, vì vậy các bạn cần hoàn thành câu hỏi để nhận điểm tối đa. Hoàn thành được câu lượng giác đề thi, học sinh cần ghi nhớ thật chắc các công thức lượng giác từ cơ bản đến nâng cao. Thời gian vừa qua, các đề thi có phương trình lượng giác với các câu hỏi không quá đánh đố, vì vậy ghi nhớ công thức lượng giác là điều kiện cần để có điểm số trong bài kiểm tra.
Các công thức lượng giác
Công thức lượng giác các cung liên quan đặc biệt


Công thức lượng giác cơ bản và công thức cộng
Các công thức lượng giác cơ bản:


Công thức cộng:

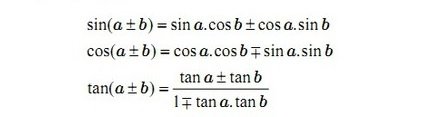
Công thức nhân đôi, nhân ba và công thức hạ bậc
Công thức nhân đôi

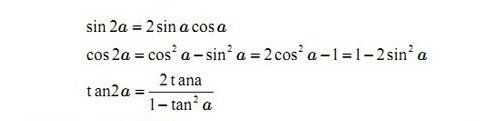
Công thức nhân ba

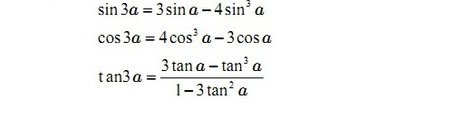
Công thức hạ bậc

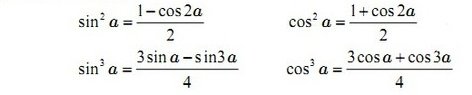
Công thức biến đổi tích thành tổng, tổng thành tích
Công thức biến đổi tổng thành tích:

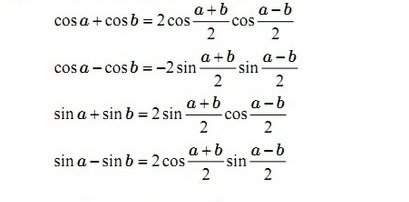
Công thức biến đổi tích thành tổng:

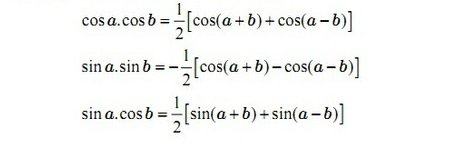
Công thức nghiệm của phương trình lượng giác cơ bản:

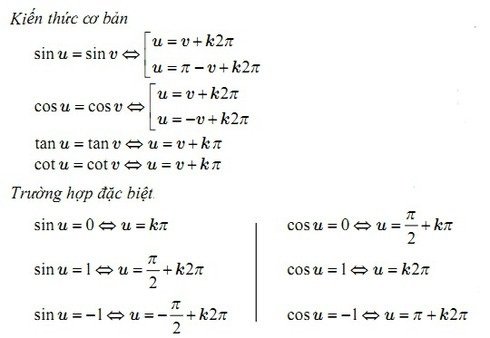


Các công thức bổ sung:


Các học thuộc công thức lượng giác
Tương tự như bên Hóa học, các công thức lượng giác khó nhớ và dễ quên. Vì vậy tìm ra phương pháp học thuộc sẽ giúp học sinh ghi nhớ dễ dàng và từ đó áp dụng giải các bài tập toán một cách hiệu quả. Sau đây chúng tôi bật mí một số các học thuộc công thức lượng giác đơn giản và dễ nhớ nhất. Theo dõi bên dưới.
Công thức cộng:
Cos + cos = 2 cos cos
cos trừ cos = trừ 2 sin sin
Sin + sin = 2 sin cos
sin trừ sin = 2 cos sin.
Sin thì sin cos cos sin
Cos thì cos cos sin sin “coi chừng” (dấu trừ).
Tang tổng thì lấy tổng tang
Chia một trừ với tích tang, dễ òm.
Hoặc:
Hàm số lượng giác
Bắt được quả tang
Sin nằm trên cos (tan@ = sin@:cos@)
Cotang dại dột
Bị cos đè cho. (cot@ = cos@:sin@)
Các cung đặc biệt
Cos đối, sin bù, phụ chéo, khác pi tan.
Cosin của 2 góc đối bằng nhau; sin của 2 góc bù nhau thì bằng nhau; phụ chéo là 2 góc phụ nhau thì sin góc này = cos góc kia, tan góc này = cot góc kia; tan của 2 góc hơn kém pi thì bằng nhau.
Công thức lượng giác nhân 3
Nhân ba một góc bất kỳ,
sin thì ba bốn, cos thì bốn ba,
dấu trừ đặt giữa 2 ta, lập phương chỗ bốn,
… thế là ok.
Công thức gấp đôi
+Sin gấp đôi = 2 sin cos
+Cos gấp đôi = bình cos trừ bình sin
= trừ 1 + 2 lần bình cos
= + 1 trừ 2 lần bình sin
+Tang gấp đôi
Tang đôi ta lấy đôi tang (2 tang)
Chia 1 trừ lại bình tang, ra liền.
Công thức biến đổi tích thành tổng:
Cos cos nửa cos-+, + cos-trừ
Sin sin nửa cos-trừ trừ cos-+
Sin cos nửa sin-+ + sin-trừ
Công thức biến đổi tổng thành tích:
sin tổng lập tổng sin cô
cô tổng lập hiệu đôi cô đôi chàng
còn tan tử + đôi tan (hoặc là: tan tổng lập tổng 2 tan)
một trừ tan tích mẫu mang thương sầu
gặp hiệu ta chớ lo âu,
đổi trừ thành + ghi sâu vào lòng
Công thức chia đôi (tính theo t=tg(a/2))
Sin, cos mẫu giống nhau chả khác
Ai cũng là một + bình tê (1+t^2)
Sin thì tử có 2 tê (2t),
cos thì tử có 1 trừ bình tê (1-t^2).
Hệ thức lượng giác tam giác vông
Sao Đi Học (Sin = Đối / Huyền)
Cứ Khóc Hoài (Cos = Kề / Huyền)
Thôi Đừng Khóc (Tan = Đối / Kề)
Có Kẹo Đây (Cotan = Kề/ Đối)
Sin : đi học (cạnh đối – cạnh huyền)
Cos: không hư (cạnh đối – cạnh huyền)
Tang: đoàn kết (cạnh đối – cạnh kề)
Cotang: kết đoàn (cạnh kề – cạnh đối)
Tìm sin lấy đối chia huyền
Cosin lấy cạnh kề, huyền chia nhau
Còn tang ta hãy tính sau
Đối trên, kề dưới chia nhau ra liền
Cotang cũng dễ ăn tiền
Kề trên, đối dưới chia liền là ra
Sin bù, cos đối, hơn kém pi tang, phụ chéo.
+Sin bù :Sin(180-a)=sina
+Cos đối :Cos(-a)=cosa
+Hơn kém pi tang :
Tg(a+180)=tga
Cotg(a+180)=cotga
+Phụ chéo là 2 góc phụ nhau thì sin góc này = cos góc kia, tg góc này = cotg góc kia.
Cách nhớ công thức: tan(a+b)=(tan+tanb)/1-tana.tanb
tan một tổng 2 tầng cao rộng
trên thượng tầng tan + tan tan
dưới hạ tầng số 1 ngang tàng
dám trừ một tích tan tan oai hùng
Xem thêm: Công thức tính diện tích tam giác
Như vậy, bên trên là bảng công thức lượng giác chi tiết và cơ bản cùng với các dạng biến đổi trong chương trình toán học. Việc ghi nhớ công thức lượng giác không dễ nhưng đã có cách học thuộc bằng mẹo giúp học sinh ghi nhớ kiến thức và giải toán lượng giác hiệu quả.
Chúc các em học tốt.
Trong toán học, lượng giác là một phần quan trọng nhất và cụ thể hơn, là các công thức lượng giác. Chúng ta có thể dễ dàng tìm thấy các bài toán liên quan đến lượng giác trong hầu hết các lĩnh vực của cuộc sống. Tuy nhiên, việc học tập và nhớ các công thức này có thể gặp phải khó khăn. Vì vậy, trong bài viết này, chúng ta đã giới thiệu và phân tích các công thức lượng giác đầy đủ và dễ nhớ nhất. Việc tổng hợp và phân tích những công thức này sẽ giúp cho việc học tập và ứng dụng trong thực tế trở nên dễ dàng hơn. Các công thức lượng giác rất hữu ích trong các bài toán toán học và thường được áp dụng trong nhiều lĩnh vực khác nhau của cuộc sống. Chúng ta nên dành thời gian để học và hiểu chúng để có thể áp dụng vào thực tế một cách hiệu quả.
Cảm ơn bạn đã xem bài viết Các công thức lượng giác đầy đủ, dễ nhớ nhất tại Thcshoanghiep.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Sinh, cosin, tan
2. Tam giác vuông
3. Công thức Pitago
4. Hệ số góc tang
5. Độ lệch giữa hai góc
6. Đơn vị độ
7. Cấp số cộng lượng giác
8. Sine rule
9. Cosine rule
10. Vị trí các góc trong các giải phẳng.






