Bạn đang xem bài viết Công thức tính diện tích tam giác: Thường, Vuông, Cân, Đều tại Thcshoanghiep.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Tam giác là một trong những hình học cơ bản và phổ biến nhất trong toán học. Tại các lớp học cấp 2, tam giác là một đề tài không thể thiếu trong chương trình học. Điều quan trọng đầu tiên khi học về tam giác là tính diện tích của nó. Tuy nhiên, vấn đề này không phải lúc nào cũng đơn giản để giải quyết, đặc biệt là khi tam giác không phải là tam giác vuông. Bài viết này sẽ giúp bạn hiểu rõ hơn về cách tính diện tích của các tam giác thường, vuông, cân và đều.
Wiki Cách Làm giới thiệu với các em học sinh các công thức tính diện tích tam giác như tam giác thường, vuông, cân, đều. Đây là cách tính diện tích tam giác phổ biến mà học sinh cần ghi nhớ trước khi làm bài tập trên lớp. Điều này giúp các em học sinh vận dụng vào bài tập mới hiệu quả nhất.

Thế nào là tam giác?
Hình tam giác là một loại hình có trong hình học: hình hai chiều phẳng có ba đỉnh là ba điểm không thẳng hàng và ba cạnh là ba đoạn thẳng. Tam giác đa giác có số cạnh ít nhất.
Phân loại tam giác
Tam giác có nhiều loại. Chúng tôi xin phân loại các tam giác như sau:
Tam giác thường: tam giác cơ bản với độ dài các cạnh khác nhau, số đo góc khác nhau. Tam giác thường trong vài trường hợp có thể gồm trường hợp đặc biệt tam giác.
Tam giác cân: có 2 cạnh bằng nhau, còn được gọi là hai cạnh bên. Tính chất tam giác cân là hai góc ở đáy luôn bằng nhau.
Tam giác đều: trường hợp đặc biệt tam giác cân với ba cạnh bằng nhau.
Tam giác vuông: là tam giác có một góc có 90 độ. Cạnh đối diện với góc vuông tên là cạnh huyền cũng là cạnh lớn nhất của tam giác. Hai cạnh còn lại có tên là cạnh góc vuông của tam giác vuông.
Tam giác tù: có 1 góc trong lớn hơn 90 độ (góc tù) hay 1 góc ngoài bé hơn 90 độ (góc nhọn).
Tam giác nhọn: tam giác có ba góc trong đều nhỏ hơn 90o (ba góc nhọn) hay có tất cả góc ngoài lớn hơn 90 độ (sáu góc tù).
Tam giác vuông cân: vừa là tam giác vuông đồng thời là tam giác cân.
Tính chất của tam giác
– Tổng các góc của tam giác bằng 180 độ (Định lý tổng ba góc trong của 1 tam giác)
– Độ dài mỗi cạnh > hiệu độ dài hai cạnh kia và nhỏ hơn tổng độ dài của các cạnh.
– Ba đường cao của 1 tam giác cắt nhau ở một điểm chúng ta gọi là trực tâm tam giác. (Đồng quy tam giác)
– Ba đường trung tuyến cắt nhau tại một điểm chúng ta gọi là trọng tâm của tam giác.
– Ba đường trung trực của tam giác cắt nhau ở 1 điểm là tâm đường tròn ngoại tiếp tam giác.
– Ba đường phân giác trong cắt nhau 1 điểm là tâm đường tròn nội tiếp tam giác.
– Định lý hàm số cosin: trong tam giác thì bình phương độ dài 1 cạnh bằng tổng bình phương độ dài hai canh còn lại trừ đi hai lần tích của độ dài hai cạnh ấy. Cosin của góc xen giữa hai cạnh đó.
– Định lý hàm số sin: trong tam giác thì tỷ lệ giữa độ dài mỗi cạnh với sin góc đối diện là như nhau với ba cạnh.
Công thức tính diện tích tam giác thường

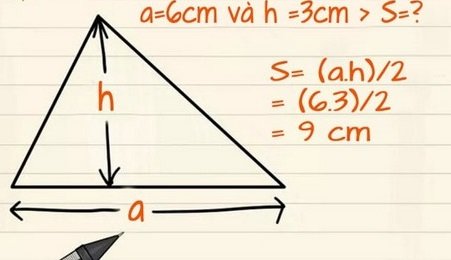
Diện tích tam giác thường tính bằng cách nhân chiều cao với độ dài đáy, lấy kết quả đó chia cho 2. Diện tích tam giác thường bằng 1/2 tích của chiều cao và chiều dài cạnh đáy tam giác.
– Công thức diện tích tam giác thường: S = (a x h)/ 2
Trong đó có:
+ a: Chiều dài đáy tam giác
+ h: Chiều cao tam giác.
– Công thức trên suy ra: h= (sx2)/a hoặc a= (sx2)/h
Chú ý:
– Lúc tính diện tích tam giác thì chiều cao tương ứng với đáy.
– Trường hợp 2 tam giác chung chiều cao hoặc chiều cao bằng nhau suy ra diện tích hai tam giác tỉ lệ với 2 cạnh đáy.
Công thức tính diện tích tam giác vuông

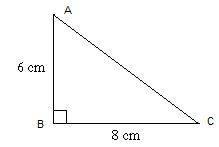
Diện tích tam giác vuông bằng 1/2 tích chiều cao với chiều dài đáy.
– Công thức tính diện tích tam giác vuông: s = (a x h)/ 2
+ a: Chiều dài đáy tam giác vuông.
+ h: Chiều cao tam giác, ứng với phần đáy chiếu lên.
– Công thức suy ra: h=(sx2)/ a hoặc a= (sx2)/h
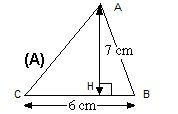
Công thức tính diện tích tam giác cân
Tam giác cân là tam giác có hai cạnh bên và hai góc bằng nhau. Để tính diện tích tam giác cân cần có các thông tin đó là chiều cao tam giác và cạnh đáy.
Diện tích tam giác cân bằng Tích chiều cao nối từ đỉnh tam giác đó tới cạnh đáy tam giác, rồi chia cho 2.
– Công thức tính diện tích tam giác cân: S = (a x h)/ 2
+ a: Chiều dài đáy tam giác cân.
+ h: Chiều cao tam giác.
Công thức tính diện tích tam giác đều

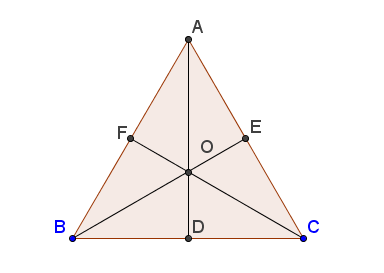
Tam giác đều là tam giác có 3 cạnh bằng nhau và mỗi góc trong tam giác đều có góc bằng 60 độ, bất cứ tam giác nào có ba góc bằng nhau được coi là một tam giác đều.
– Công thức tính diện tích tam giác đều: S = A2 X (√3)/4
Trong đó có:
a: đó là chiều dài cạnh bất kỳ trong tam giác đều.
Công thức tính diện tích khác
Dùng hình học
Diện tích S sẽ có công thức bằng ½bh.
Với b là độ dài cạnh bất kỳ trong tam giác (hay đáy)
Với h là độ dài đường cao khi hạ từ đỉnh đối diện xuống cạnh đó.

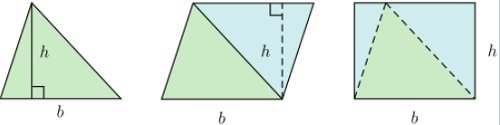
Từ tam giác ta sẽ sao y 1 tam giác bằng nó, sau đó quay góc 180°, và ghép thành hình bình hành. Cắt 1 phần hình bình hành, ghép tạo thành hình chữ nhật. S hình chữ nhật là bh, nên diện tích tam giác là ½bh.
Diện tích tam giác bằng độ dài cạnh đáy nhân với chiều cao chia 2:
S=1/2bh
Riêng tam giác vuông: diện tích là 1 nửa tích hai cạnh góc vuông.
Vừa rồi là những kiến thức cơ bản về cách tính diện tích tam giác: Thường, Vuông, Cân, Đều trong hình học mà bạn nên nắm rõ trước khi làm bài tập tại lớp hoặc trong sách bài tập. Hãy nắm rõ các công thức cơ bản bên trên bạn sẽ làm bài tập chuẩn xác nhất. Chúc các bạn học tốt!
Tổng kết lại, công thức tính diện tích tam giác là rất quan trọng và được sử dụng rộng rãi trong toán học cũng như trong đời sống thực tế. Để tính diện tích tam giác, ta cần biết chiều dài và chiều rộng của tam giác và sau đó áp dụng công thức tính diện tích tương ứng. Công thức tính diện tích tam giác thường, vuông, cân, đều có thể được sử dụng dựa trên cấu trúc của tam giác đó. Với kiến thức này, chúng ta có thể tính toán diện tích của tam giác dễ dàng hơn và sử dụng nó để giải quyết nhiều vấn đề trong tất cả các lĩnh vực của cuộc sống.
Cảm ơn bạn đã xem bài viết Công thức tính diện tích tam giác: Thường, Vuông, Cân, Đều tại Thcshoanghiep.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Tam giác thường
2. Tam giác vuông
3. Tam giác cân
4. Tam giác đều
5. Diện tích tam giác
6. Công thức tính diện tích tam giác
7. Định lý Pythagoras
8. Tính chu vi tam giác
9. Tam giác góc nhọn
10. Tam giác góc tù






