Bạn đang xem bài viết Toán học: Lăng trụ tam giác đều tại Thcshoanghiep.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Trong lĩnh vực toán học, lăng trụ tam giác đều là một trong những chủ đề được quan tâm nhiều. Lăng trụ tam giác đều là một hình học được hình thành từ một tam giác đều xoay quanh một trong các cạnh của tam giác đó để tạo thành một hình trụ. Với tính chất đặc biệt của mình, lăng trụ tam giác đều đóng góp rất nhiều vào các nghiên cứu và ứng dụng trong thực tế. Hãy cùng đi tìm hiểu về lăng trụ tam giác đều thông qua bài viết sau đây.
Hình học không gian là một trong những môn học quan trọng của toán học. Trong hình học không gian có rất nhiều dạng khác nhau. Hôm nay, hãy cũng mình tìm hiểu về lăng trụ tam giác đều nhé! Qua bài dưới đây, bạn sẽ được sơ lược lại về định nghĩa, tính chất và một số công thức của hình lăng trụ và hình lăng trụ đứng. Đồng thời, học thêm về các công thức tính của hình lăng trụ tam giác đều. Bao gồm các công thức: tính diện tích đáy của hình lăng trụ tam giác đều, tính diện tích xung quanh của hình lăng trụ tam giác đều và tính thể tích của hình lăng trụ tam giác đều.
Đầu tiên, để biết được lăng trụ tam giác đều là gì, hãy cũng mình tìm hiểu về khái niệm hình lăng trụ và lăng trụ đứng nhé.
1) Hình lăng trụ và hình lăng trụ đứng.
a) Định nghĩa và công thức về hình lăng trụ
Trong toán học không gian, hình lăng trụ được xác định là một loại đa diện. Loại đa diện này có 2 mặt đáy là các đa giác phẳng. Còn cách mặt còn lại của hình lăng trụ là các hình bình hành.
Theo công thức toán học, thể tích của hình lăng trụ sẽ được tính như sau:
V=B.h
Trong đó:
- V là thể tích hình lăng trụ.
- B là diện tích của mặt đáy.
- h là khoảng cách giữa 2 mặt đáy/chiều cao hình lăng trụ.
b) Định nghĩa và công thức về hình lăng trụ đứng
Hình lăng trụ đứng được xác định là hình lăng trụ có cạnh bên và mặt đáy vuông góc với nhau.
Thuật ngữ: Thông thường thì ta gặp hình lăng trụ đều có đáy là tam giác hoặc hình vuông trong nhiều bài toán. Người ta thường gọi tắt trường hợp đó với các thuật ngữ là hình lăng trụ tam giác đều, lăng trụ tứ giác đều.
Các tính chất cơ bản của hình lăng trụ đứng bao gồm:
- Mặt bên của hình lăng trụ đứng là hình chữ nhật.
- Tất cả các mặt bên của hình lăng trụ đứng đều vuông góc với đáy.
Theo công thức toán học, diện tích của hình lăng trụ đứng được tính như sau:
- Diện tích xung quanh của lăng trụ đứng = Tổng diện tích các mặt bên = (Chu vi đáy)x(Chiều cao)
- Diện tích toàn phần của lăng trụ đứng = Tổng diện tích các mặt bên và diện tích 2 đáy.
Cũng theo công thức toán học, diện tích hình lăng trụ đứng vẫn được tính theo công thức:
V = B.h
Trong đó,
- V là thể tích hình lăng trụ.
- B là diện tích của mặt đáy.
- h là chiều cao hình lăng trụ.
2) Hình lăng trụ tam giác đều
a) Định nghĩa hình lăng trụ tam giác đều
Hình lăng trụ tam giác đều được xác định là hình lăng trụ đứng với đáy là tam giác đều.
Hình mô tả của hình lăng trụ tam giác đều:

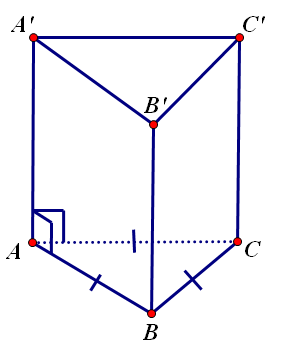
Như vậy, hình lăng trụ tam giác đều sẽ có các tính chất cơ bản sau:
- Hai đáy là hai tam giác đều và bằng nhau.
- Các mặt bên là các hình chữ nhật bằng nhau.
- Các mặt bên và hai đáy vuông góc với nhau.
b) Các công thức toán học của lăng trụ tam giác đều
Theo toán học, lăng trụ tam giác đều có các công thức như sau:
- Diện tích đáy: S = a2 . (√3)/4.
Trong đó, a là chiều dài cạnh đáy của lăng trụ tam giác đều.
- Diện tích xung quanh của lăng trụ tam giác đều = Tổng diện tích các mặt bên = (Chu vi đáy) x (Chiều cao) : S = 3.a.h.
- Diện tích toàn phần của lăng trụ tam giác đều = Tổng diện tích các mặt bên và diện tích 2 đáy: S = 3.a.h + a2 . (√3)/4.
Trong đó, a là chiều dài cạnh đáy của lăng trụ tam giác đều, h là chiều cao của lăng trụ tam giác đều.
- Thể tích của lăng trụ tam giác đều = (Diện tích đáy) x (Chiều cao): V = a2 . (√3)/4 . h
Trong đó, a là chiều dài cạnh đáy của lăng trụ tam giác đều, hi là chiều cao của lăng trụ tam giác đều.
c) Một số bài tập về hình lăng trụ tam giác đều
Bài tập 1: Cho hình lăng trụ tam giác đều ABC.A’B’C’ (đáy là tam giác ABC và A’B’C’) với chiều dài cạnh đáy AB của hình lăng trụ này là 4 cm. Đồng thời, biết được diện tích của hình tam giác A’BC là 8 cm2 . Hãy xác định chiều cao và thể tích của khối lăng trụ này.
Bài tập 2: Cho hình lăng trụ tam giác đều ABC.A’B’C’ (đáy là tam giác ABC và A’B’C’) với chiều cao AA’ của hình lăng trụ là 2 cm và diện tích của hình tam giác A’BC là 8 cm2 . Hãy xác định chiều dài cạnh đáy, diện tích đáy, diện tích toàn phần và thể tích của khối lăng trụ này.
Bài tập 3:
Tính thể tích V của khối lăng trụ tam giác đều ABC.A’B’C’ có AA′=BC=a.AA′=BC=a.
A. V=a33√12V=a3312
B. V=a33√4V=a334
C. V=a32√6V=a326
D. V=a33
Đáp án đúng: B
Lý giải: ABC là tam giác đều cạnh nên: SABC=a23√4.SABC=a234.
Khi đó VABC.A′B′C′=SABC.AA′=a33√4.VABC.A′B′C′=SABC.AA′=a334.
Bài tập 4: Tính thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a.
A. a32a32
B. a33√2a332
C. a33√4a334
D. a33√12a3312
Đáp án đúng: C
Lý giải: Khối lăng trụ của đáy là tam giác đều cạnh a, chiều cao h=a. Nên suy ra có thể tích là: V=Sday.h=a23√4.a=a33√4
Bài tập 5: Cho hình hộp chữ nhật ABCD.A’B’C’D’ với AB=3cm; AD=6cm và độ dài đường chéo AC’=9cm . Tính thể tích V của hình hộp ABCD.A’B’C’D’?
A. V=108cm3V=108cm3
B. V=81cm3V=81cm3
C. V=102cm3V=102cm3
D. V=90cm3V=90cm3
Đáp án đúng: A
Lý giải: Ta có: AC=BD=AB2+AD2−−−−−−−−−−√=35√AC=BD=AB2+AD2=35
CC′=AC′2−AC2−−−−−−−−−−√=6CC′=AC′2−AC2=6
Vậy thể tích hình hộp là:VABCD.A′B′C′D′=3.6.6=108
Hi vọng các thông tin trên đây sẽ giúp ích cho bạn trong môn hình học không gian. Các công thức toán học về diện tích và thể tích của hình lăng trụ tam giác đều trên đây sẽ giúp bạn tính toán nhanh hơn. Chúc bạn học tập hiệu quả hơn nhé!
Trong bài viết này, chúng ta đã tìm hiểu về lăng trụ tam giác đều. Đây là một dạng lăng trụ đặc biệt, với các đặc tính riêng biệt và đáng chú ý. Chúng ta đã nghiên cứu về các đường chéo, biên và thể tích của lăng trụ tam giác đều. Bên cạnh đó, chúng ta cũng đã áp dụng kiến thức quan trọng của toán học, như hình học và tính diện tích, để giải quyết vấn đề liên quan đến lăng trụ này. Như vậy, chúng ta có thể thấy rằng toán học không chỉ là một công cụ hữu ích trong cuộc sống thực tế, mà còn là một nguồn cảm hứng và niềm đam mê đối với những ai yêu thích môn học này.
Cảm ơn bạn đã xem bài viết Toán học: Lăng trụ tam giác đều tại Thcshoanghiep.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Tam giác đều
2. Diện tích tam giác
3. Đường cao của tam giác
4. Lăng trụ
5. Hình hộp chữ nhật
6. Thể tích hình lăng trụ
7. Góc giữa hai mặt phẳng
8. Phương trình mặt phẳng
9. Định lý Pytago
10. Trung điểm tam giác.






